ABOUT

Mathematical models and methods are indispensable in natural and engineering sciences. The research training group "IntComSin" combines the expertise at FAU Erlangen- Nürnberg and at University of Regensburg in (S)PDE-analysis, calculus of variations, homogenisation and Gamma-convergence, numerical analysis and scientific computing to set up a unique research and training center to investigate at the highest scientific level selected phenomena and processes, which are related to interfaces, multiple scales/fields, and dimension reduced models arising as singular limits. This way, the research training group responds to the still growing demand for refined mathematical models, their thorough analysis and efficient numerical implementation, their predictive power and potential of optimisation which arises in various fields of natural sciences, medicine, and engineering (biology, cardiology and oncology, materials sciences, manufacturing technology). Questions under consideration are currently of major interest both from a mathematical point of view and from an application perspective and are related to the guiding topics of the RTG:

	Interfaces Interfaces separating states of different properties are ubiquitious in the sciences. Examples are fluid-structure interactions in arterial blood flow, two-phase flows, or free boundaries in tumor growth as well as in the macroscopic behaviour of interacting species. Modern methods from the theory of abstract evolution equations, from calculus of variations, or from (geometric) measure theory lay the ground for a systematic mathematical theory. Similarly, numerical methods based on parametric approaches, level sets or phase-fields are now sufficiently mature to deal with challenging phenomena. In many applications, intricate couplings occur between equations defined on the interface and equations defined in the surrounding bulk phases, which so far are only partially understood. The exploration of problems related to these questions shall be continued within the second funding period of the RTG.
	Complex Structures Porous media, elastic media with fine-scale structures, or non-classical fluids, for which the presence of microstructures -- like polymers -- causes non-standard flow behaviour -- these are typical examples for "complex structures" to be investigated in the RTG. On the level of modeling, such phenomena involve multiple scales, arising, e.g., as fine-scale structures in the geometry or as rapidly oscillating coefficients in the governing partial differential equations. The analysis and the numerics of these phenomena are well-developed in simple situations, and some realistic complex phenomena have been studied in the first funding period of the RTG. Topics to be investigated in the second period include characteristic features of viscoelastic fluids and micro-macro effects in porous media involving dynamic interfaces or reactive transport of multiply charged species.
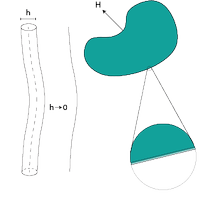
	Singular limits & Dimension reduction Small length or time-scales are characteristic for many problems in the sciences. By singular limit theory, it is possible to formally derive dimension reduced models which are often computationally less complex. Prominent examples are different shell and plate theories arising as singular limits in the three-dimensional theory of nonlinear elasticity. Two-phase flows, homogenisation in porous media, and boundary or interior layers in fluid dynamics are typical as well. However, many limits can only be studied formally so far. Hence, one of the goals of the RTG is to justify corresponding arguments with the help of rigorous analysis. From the numerics perspective, the discretization of problems with small parameters leads to large and stiff systems which are in need of new numerical methods. Further scientific aspects related to this thematic area are analytical and numerical studies of dimension-reduced models occurring as singular limits.

RTG IntComSin -- structural aspects
In the second funding period, up to 40 scientists -- including the thirteen principal investigators as well as doctorate and post-doctorate researchers funded from other sources -- will contribute to the success of the RTG. Their research is grouped around seven research fields: Interaction at Interfaces (RF1), Flow and Transport in Porous Media (RF2), Dimensional Reduced Models for Thin Structures (RF3), Growth Models with Elastic Stress (RF4), Multi-Phase and Multi-Field Aspects in Fluid Flow (RF5), Micro-Macro Aspects of Fluid Flow (RF6), Variational Models for Shapes and Interfaces (RF7).

RTG IntComSin -- training aspects
The doctoral programme offers a structured course programme addressing advanced topics in partial differential equations, calculus of variations, numerical analysis, scientific computing, mathematical modeling, and professional skills. Doctoral projects are generally supervised by two scientists with complementary specializations, and experienced doctoral researchers act as mentors for new fellows. Doctoral researchers of the Research Training Group benefit from numerous possibilities of scientific exchange both on the national and on the international level.